Edit Distance
AfterAcademy Tech
•
06 Apr 2020

Asked in: Amazon, Google, Microsoft
Difficulty: Hard
Understanding the problem
Problem description
Given two strings string1, string2 and some edit operations. Write an algorithm to find the minimum number of operations required to convert string1 to string2.
The allowed operations are:
- Insertion — Insert a new character.
- Deletion — Delete a character.
- Substitution — Replace one character by another.
Example 1 —
Input : string1 = "horse", string2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')
Example 2
Input : string1 = "intention", String2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')
You may first try to solve this problem here.
Solutions
We will be discussing three solutions to the problem. We will start with brute force and try to optimize the solution.
- Brute Force Approach: This is a simple recursive solution where we will solve the problem via the solution of its sub-problems.
- Memoization Approach: Here, we will calculate the overlapping problems and will save it for future use.
- Tabulation Approach: This is the most optimized solution which uses iteration to calculate the result based on the bottom-up approach.
1. Brute Force Approach
Here we will discuss a simple solution based on recursion. For using recursion, we should think about the smaller sub-problem which can be solved easily. By making the following observation we can reduce our task of calculating the entire combination of changes and leave this to recursion→
When we recurse over the input sequence, we’re essentially going to be saying “figure out what to do with the first character,
then compute the result by adding together the cost of that and everything that comes after”.
From this, we can deduce that we’re going to be working with suffixes.
Solution steps
- Consider i and j be the pointers to the string1 and string2 respectively.
- if the first character of both strings is the same then recurse for lengths i+1 and j+1.
- Otherwise, we will perform all the three operations on the ith character of the first string and recursively compute the minimum cost among them.
- The result will be the minimum of these three operations.
- Insertion: Recur for i and j+1
- Deletion: Recur for i+1 and j
- Substitution: Recur for i+1 and j+1
Pseudo Code
// Driver function
int editDistance(String word1, String word2) {
if (word1 == null || word1.length() == 0)
return word2.length()
if (word2 == null || word2.length() == 0)
return word1.length()
return match(word1, word2, 0, 0)
}
// Helper function
int match(String s1, String s2, int i, int j) {
//If one of the string's pointer have reached the end of it
if (s1.length() == i)
return s2.length() - j
if (s2.length() == j)
return s1.length() - i
int result
// If current poisition is the same.
if (s1[i] == s2[j]) {
result = match(s1, s2, i + 1, j + 1)
} else {
//Case1: insert
int insert = match(s1, s2, i, j + 1)
//Case2: delete
int delete = match(s1, s2, i + 1, j)
//Case3: substitute
int substitute = match(s1, s2, i + 1, j + 1)
result = min(insert, delete, substitute) + 1
}
return result
}
Complexity Analysis
In the worst case, we have three choices for every step.
Time Complexity: O(3^n) (Why?)
Space Complexity: O(m), where m is the stack space of the recursion tree.
Critical Ideas to Think
- Can you figure out what could be the worst-case for this approach?
- Can we draw the recursive tree for this solution?
- How are we handling all the three operations?
2. Memoization Approach
Why Memoization? If you look at the below recursion tree then you will find that there are many subproblems that are overlapping.
So, when we calculate the optimal value for particular ith and jth index of string1 and string2 respectively, we could store the value in a cache array so that it could directly be used if needed.
Define problem variables and decide the states
There are two parameters on which the state of the problem depends that is the indices of string1 and string2.
Storing result
Since we have seen in order to retrieve the already calculated results in O(1), we need to store them. For storage we require memory but how much memory do we actually require? First, we must see the optimal substructure of the problem →
Optimal Substructure
Suppose we know the edit distance of the two strings until i and j indices. Then we can write →
editDistance(i+1, j+1) = 1 + min(editDistance(i,j+1), editDistance(i+1, j), editDistance(i,j))
Recursive tree visualization
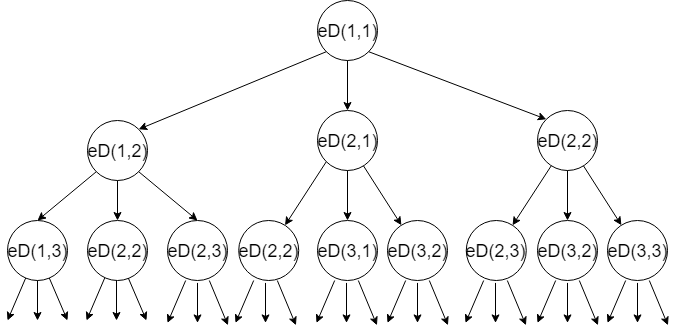
The above diagram represents the recursive structure of edit distance (eD). The parameters represent the i and j pointers. Now you may notice the overlapping subproblems. Eg. eD(2, 2)
Space Required
Since we are storing result for every pair of i and j indices of both strings, so in the worst case we will require an array of size len(string1)*len(string2)
Here we will see the memoization solution steps:-
- check if the character at string1[i] is equal to string2[j] then look for cache[i+1][j+1]
- Otherwise, take minimum of cache[i+1][j], cache[i][j+1], cache[i][j] and add 1 to it, Store the result in cache[i+1][j+1]
Pseudo code
int editDistance(String s1, String s2) {
int cache[s1.length][s2.length]
for (int i = 0; i < s1.length; i++) {
for (int j = 0; j < s2.length; j++) {
cache[i][j] = -1
}
}
return match(s1, s2, 0, 0, cache)
}
int match(string s1, string s2, int i, int j, int[][] cache){
if (s1.size() == i)
return s2.size() - j
if (s2.size() == j)
return s1.size() - i
if (cache[i][j] != -1) {
return cache[i][j]
}
if (s1[i] == s2[j]) {
cache[i][j] = match(s1, s2, i + 1, j + 1, cache)
} else {
//Case1: insert
int insert = match(s1, s2, i, j + 1, cache)
//Case2: delete
int delete = match(s1, s2, i + 1, j, cache)
//Case3: replace
int replace = match(s1, s2, i + 1, j + 1, cache)
cache[i][j] = min(insert, delete, replace) + 1
}
return cache[i][j]
}
Complexity analysis
Now we could have almost n*m operation for each pair of ith and jth index where n and m are the lengths of string1 and string2 respectively.
Time Complexity — O(n²)
Space Complexity — O(n²)
Critical Ideas to Think
- Why this solution is a bottom-up approach?
- Do you recognize the optimization of overlapping subproblems?
3. Tabulation Approach
Tabulation is the most optimized solution and works in a bottom-up approach, it comes after we have done memoization. Since it is quite clear that this problem has dependencies on smaller problems discussed in the above section.
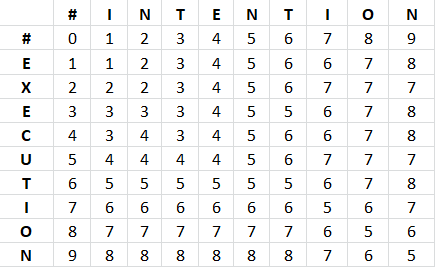
So, Before calculating f(i,j) where f is the editDistance function and i, j are the respective indices pointer on the two strings, it would be good if we calculate f(i, j-1), f(i-1, j) and f(i-1, j-1). Refer to the below structure
The answer for f(i,j) would be the minimum from (f(i-1, j),f(i, j-1),f(i-1, j-1))+1
Similarly for other values see the table filling below.
Iterative Structure for Table-filling
Considering the above example

Pseudo Code
int editDistance(string word1, string word2) {
int n1 = word1.size()
int n2 = word2.size()
int matched[n1+2][n2+2]
for(int i=0 to i <= n1)
{
matched[i][0] = i
}
for(int i=0 to i <= n2)
{
matched[0][i] = i
}
for(int i=1 to i <= n1)
{
for(int j=1 to j <= n2)
{
if(word1[i-1] == word2[j-1])
{
matched[i][j] = matched[i-1][j-1]
} else {
matched[i][j] = 1+min(matched[i-1][j],min(matched[i][j-1], matched[i-1][j-1]))
}
}
}
return matched[n1][n2]
}
Complexity Analysis
Time Complexity: O(n²) (Why?)
Space Complexity: O(n²)
Critical Ideas to Think
- How we are handling all the three operations incase of different characters of both strings?
- Can you see that subproblems are solved using iteration?
- Do you think that the tabulation approach is the same as of memoization approach?
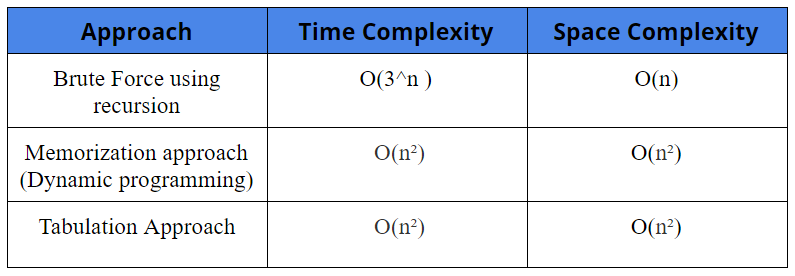
Comparison of different solutions
Suggested Problems to Solve
- Delete Operation for Two Strings
- Minimum ASCII Delete Sum for Two Strings
- Find longest common subsequence
- Minimum distance to the end of a grid from source
Happy Coding!
