Dijkstra’s Algorithm

We have already discussed Graphs and Traversal techniques in Graph in the previous blogs. To continue with graphs, we will see an algorithm related to graphs called Dijkstra’s Algorithm which is used to find the shortest path between source vertex to all other vertices in the Graph. So let’s get started.

Prerequisites

• Introduction to Graph in Programming
• Graph Traversal: Depth First Search
• Graph Traversal: Breadth-First Search

Shortest Path Algorithms

There are many algorithms in Graph which are used to find the shortest path between vertices of the graph like Bellman Ford’s Algorithm, Dijkstra’s Algorithm, Floyd–Warshall’s Algorithm, etc.

The shortest path is about finding a path between 2 vertices in a graph such that the sum of weights of all edges that are coming in the path should be minimum.

In the unweighted graph, this problem can be solved using BFS. (Think!)

Dijkstra’s Algorithm

There are many use cases of Dijkstra’s Algorithm but the most common use case of it is to find the shortest path from the source vertex to all other vertices in a graph.

In this algorithm, we generate a shortest-path tree. We maintain two sets S1 and S2, S1 for the vertices that are included in the tree and S2 for the remaining (or yet to be included in the tree). At each step of the algorithm, we find a vertex from S2 that has a minimum distance from the source.

Let’s take a look at the steps, and then we will see the illustration with an example.

• For set S1 and S2, we will use a boolean array where vis[i] will denote whether vertex i is added to set S1 or not. Initially, all elements are false, which will denote the empty set S1.
• We will also store the weight of the path from the source vertex in an array. Initially, all the weights will be INFINITE except the source vertex which will be 0.
• Now we will perform the following operation till all the vertices are visited.

→ Pick a vertex u which is not visited and has minimum distance value.

→ Mark that vertex as visited.

→ Update all the distance values of the vertex that are adjacent to u only if it is lesser than the old value.

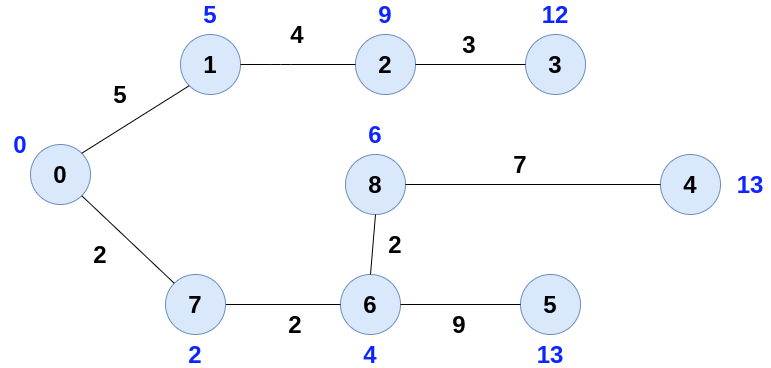
Illustration

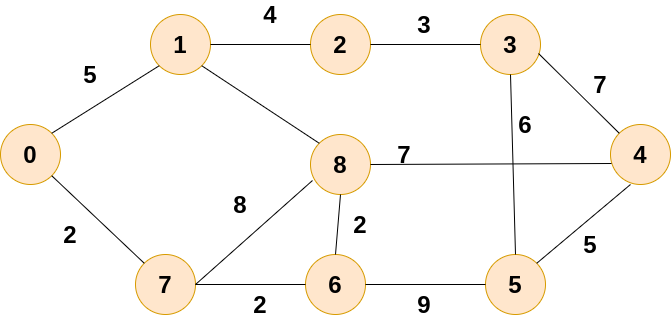
Let's consider the following graph. We need to find the shortest distance to all vertices from source vertex i.e. 0.

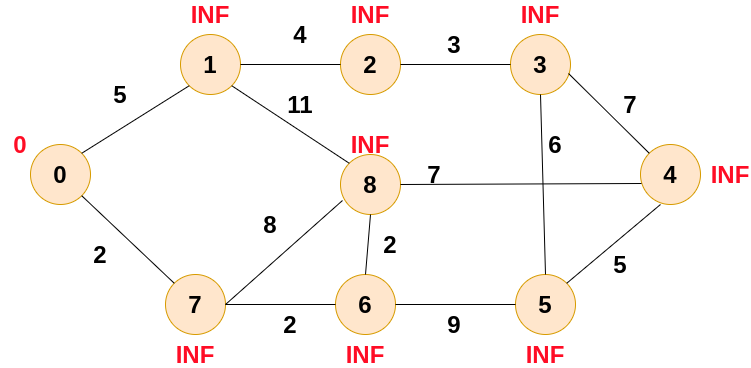
Now, we will assign the weight to these vertices. We will assign infinite values to all except for source vertex.

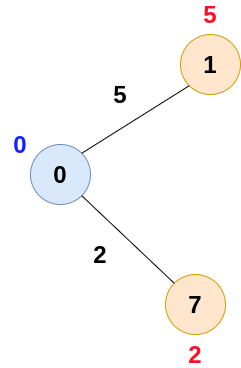
Now, start constructing the shortest path tree, we will take the vertex with the minimum weight and also update the weights of the neighbours of that vertex.

Keep updating the same till we cover all the nodes.

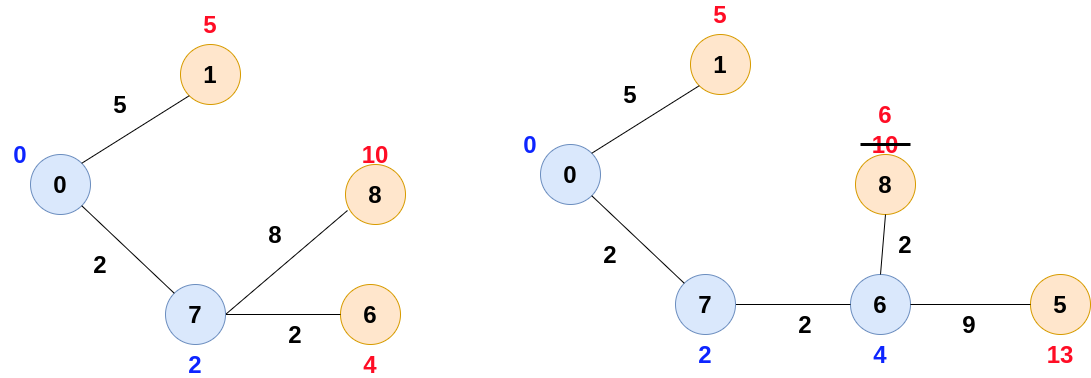
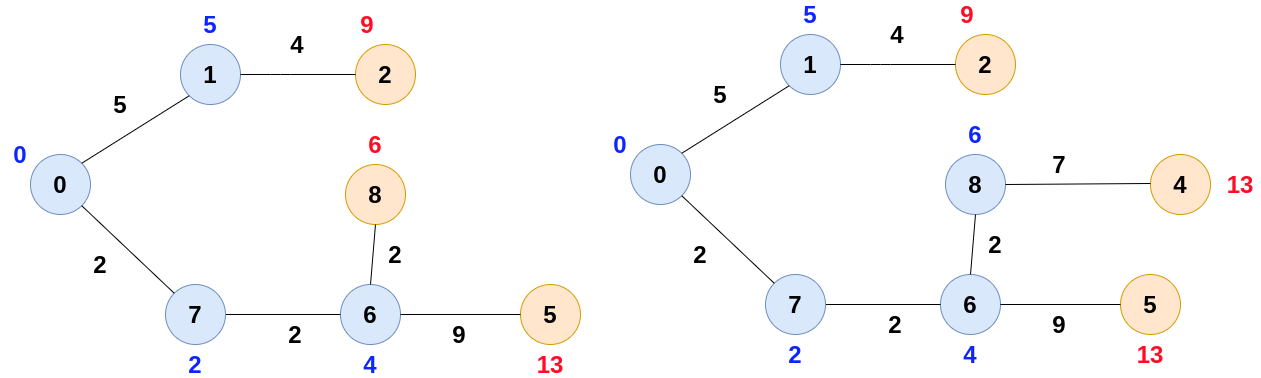
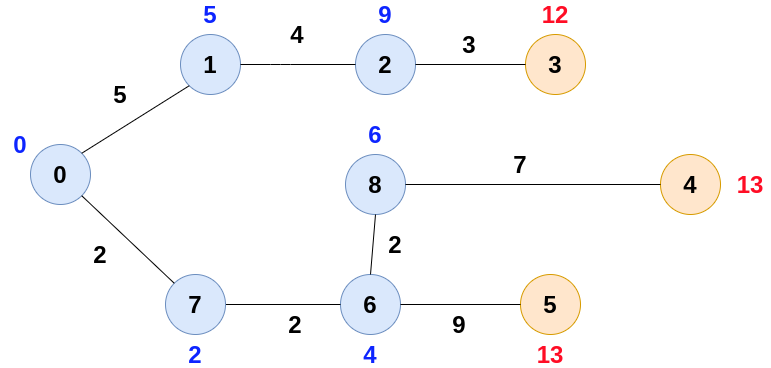
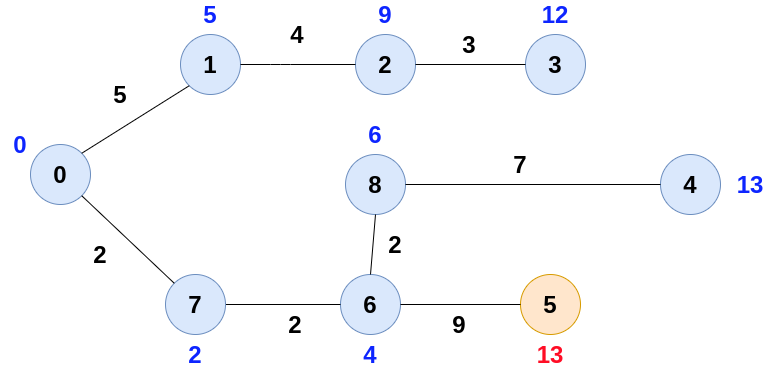
Note:- When two nodes have equal weights, we can give priority to anyone.

Pseudo Code

int minWeight(int weight[], bool vis[], int V)
{
    min = inf, min_index = -1
    
    for( i = 0 to V )
    {
        if( vis[i] == false and weight[i] < min)
        {
            min =weight[i]
            min_index = i
        }
    }
    return min_index
}
int[] dijsktra(int graph[V][V], int V, int src)
{
    bool vis[]
    int weight[]
    
    for(i = 0 to V)
    {
        vis[i] = false
        weight[i] = inf
    }
    
    weight[src] = 0
    
    for(i = 0 to V)
    {
        u = minWeight(weight, vis, V)
        
        vis[u] = true
        
        for(v = 0 to V)
        {
            if(!vis[v] and graph[u][v] != 0 
                and weight[u] + graph[u][v] < weight[v])
            {
                weight[v] = weight[u] + graph[u][v]
            }
        }
        
    }
    return weight;
}

Critical Ideas to Think

• The above approach only calculates the shortest distance. Can u find out how the path information can also be retrieved? (Hint - Prim’s)
• The time complexity of the above solution is O(V²). Can it be reduced to O(E log V) if the adjacency list is given as input? (Hint — Think of binary heap or Priority Queue)
• The above approach is for an undirected graph. Can it be used for a directed graph? (Ans - Yes!!)
• It will not work if the vertex has negative edges. Can you think why? (Hint - There is an algorithm for that “Bellman-Ford”)

Graph questions

• Is Graph Bipartite?
• Number of Islands
• Word Ladder Problem
• Smallest Multiple with 0 and 1
• Course Schedule
• Knight on Chessboard

Happy Learning, Enjoy Algorithms!

Team AfterAcademy!