Detect and Remove Loop In A Linked List

Detect and Remove Loop in a Linked List

Difficulty: Hard

Asked in: Amazon, Microsoft

Understanding The Problem

Problem Description

You are given the head of a linked list which probably contains a loop. If the list contains a loop, you need to find the last node of the list which points to one of its previous nodes to create a loop and make it point to NULL, thereby removing the loop.

Problem Note:

It’s possible that the linked list does not contain a loop
Do not use extra space

Example 1

Input:   1 -> 2 -> 3 -> 4 -> 5
                   |         |
                   |         |    
                   - - - - - -
Output:  1 -> 2 -> 3 -> 4 -> 5
Explanation: The node 5 at the end of loop points to 3 and creates a loop. We make it point to NULL and remove the loop.

Example 2

Input: 2 -> 20 -> 6 -> 19 -> 13 -> 4
Output: 2 -> 20 -> 6 -> 19 -> 13 -> 4
Explanation: No loop present.

Solutions

We will be discussing two different solutions to this problem.

Using Hashing : Store each node in a set until there are no new nodes available and the first node which is already in the set will be the start of the loop.
Using Mathematics: Find total nodes in the loop and then head-start a pointer from that many nodes from the head node. Now, start another pointer from the head node at an equal pace and look for the point where they meet.

The node structure passed to the function will be

class Node { 
    int data
    Node next 
}

You can try the problem here .

1. Hashing

This problem asks us to check if there’s a loop inside the linked list and if so, we have to remove the loop without losing any nodes, which means we have to remove the link of the first repeating node.

So, a very simple idea is to use a hash set to store all the nodes of the linked list until there’s a repeating node. We are familiar with the concept that lookup time in a set is of constant time which can help us in optimizing the time complexity.

If the set has all the nodes of the linked list and the head pointer is now pointing to NULL, then obviously that means there is no loop.

Solution Step

Create a hash set, nodeSet
Create a reference pointer ptr pointing to head .
Move the ptr forward until ptr.next is not NULL or ptr.next is not present in nodeSet
If we encounter ptr.next already present in hashSet then set ptr.next to NULL

Pseudo Code

// driver function
void detectAndRemoveLoop(Node head) 
{ 
    // If list is empty or has only one node without loop
    if (head == NULL or head.next == NULL) 
        return
    Node ptr1 = head
    set hashSet
    hashSet.add(ptr1)
    while(not hashSet.contains(ptr1.next) or ptr1 is not NULL){
        hashSet.add(ptr1)
        ptr1 = ptr1.next
    }
    // if ptr1 is not NULL then it ptr1.next must be the start of loop
    if(ptr1){
        ptr1.next = NULL
    }
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(n)

Critical Ideas To Think

How did we make sure that there is a loop inside the linked list or not in this approach?
Why is the first repeating node already available in the hashSet represent the start of the loop?

2. Using Maths

The previous approach was working in linear time. However, the problem explicitly asked us to solve using constant extra space.

So, We will first have to check if there’s a loop inside the linked list. For that, we can use the concept of the slow and fast pointer or Floyd Cycle Detection algorithm. We will take two pointers, say slow and fast pointing to the head of the linked list. Now ascend slow by one and fast by two in each iteration. If any of the pointers reaches to NULL then there’s no cycle otherwise, at some point slow and fast will point to the same node and that will prove there is a cycle inside the linked list.

Now, Confirming there’s a cycle in the linked list, we will have to identify the node from where the loop first originates. To do that let’s try some maths.

Consider a linked list of some nodes which also contains a loop.

First, identify the length of the loop. Use slow and fast pointer and move them until they point to the same node. Now keeping slow pointer constant, move the fast pointer by one until it reaches to slow pointer again, thereby giving the length of the loop. Say, the length of the loop is D

Our goal is to find X, i.e. distance from head to the beginning of the loop. Such that we can change (X + D)th node’s next from head to NULL and remove the loop.
Take two-pointers and point them to the head. say ptr1 and ptr2

Now, Move Ptr2 by D nodes. Where D = length of cycle

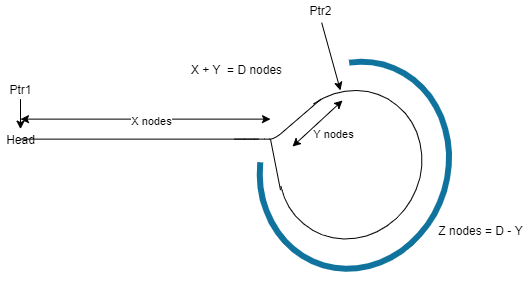
Let’s do some math

Length of loop is D
Looking at the above diagram, Ptr2 is moved D distance from head.
=> X + Y = D   -- eqn 1
and let's assume Ptr2 is Z nodes away from start of loop.
=> Z = D - Y   -- eqn 2

Equating eqn 1 and eqn 2
=> X + Y = Z + Y
=> X = Z

This proves, moving Ptr1 (from Head ) and Ptr2 (Y dist away from the start of loop) at the same pace will always collide at the node where the loop begins.

Solution Steps

Take two pointers slow and fast and increment them by one and two respectively until they meet, signifying the existence of a loop.
Fix the slow pointer and move the fast pointer by one step, such that it visits each node of the loop while stating the total number of nodes(D) inside the loop.
Take two pointers ptr1 and ptr2 pointing to head
Move ptr2 by D nodes.
Now, increment ptr1 and ptr2 by the equal pace until ptr2.next != ptr1.next
Now, set Ptr2.next to NULL

Pseudo Code

// driver function
void detectAndRemoveLoop(Node head) 
{ 
    // If list is empty or has only one node without loop
    if (head == NULL or head.next == NULL) 
        return
    Node slow = head, fast = head
    slow = slow.next
    fast = fast.next.next
    // Check if loop exists
    while (fast and fast.next) { 
        if (slow == fast)
            break
        slow = slow.next 
        fast = fast.next.next
    }
    if(slow == fast) {    
        int length_of_loop = 1
        while(fast.next != slow){
            fast = fast.next
            length_of_loop = length_of_loop + 1
        }
        removeLoop(head, length_of_loop)
    }
}
// utility function
void removeLoop(Node head, int D) {
    Node ptr1 = head
    Node ptr2 = head
    while(D > 0){
        ptr2 = ptr2.next
        D = D - 1
    }
    while(ptr1.next != ptr2.next) {
        ptr1 = ptr1.next
        ptr2 = ptr2.next
    }
    // Remove loop
    ptr2.next = NULL
    return
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(1)

Critical Ideas To Think

How did we make sure that there is a loop inside the linked list or not in this approach?
How did we find the number of nodes X in the above diagram?
How did we make sure that moving ptr2 and ptr1 at the same pace will definitely meet at the beginning of the node?