Convert A Min Heap to Max Heap

Convert A Min Heap To Max Heap

Difficulty: Medium

Asked in: Google

Understanding The Problem

Problem Description

Given array representation of min Heap , write a program to convert it to max Heap . The expected time complexity is O(n).

Example

Input: A[] = [3 5 9 6 8 20 10 12 18 9]

         3
      /     \
     5       9
   /   \    /  \
  6     8  20   10
 /  \   /
12   18 9

Output: A[] = [20 18 10 12 9 9 3 5 6 8] or any Max Heap formed from input elements

         20
       /    \
     18      10
   /    \    /  \
  12     9  9    3
 /  \   /
5    6 8

You may attempt the problem here.

You should read about the introduction of heaps from here .

Solution

Our final goal is to only build the max heap and the problem expects the solution to be in O(n) time complexity. The idea is very simple, we simply build Max Heap without caring about the input.

We start from the bottom-most and rightmost internal node of min Heap and then heapify all internal modes in the bottom-up way to build the Max heap.

Why this method will work?

To build a heap, the following algorithm is implemented for any input array.

BUILD-HEAP(A) 
    heapsize := size(A)
    for i := floor(heapsize/2) downto 1 
        do HEAPIFY(A, i)
    end for 
END

A quick look over the above algorithm suggests that the running time is O(n log n) since each call to heapify costs O(log n) and Build-Heap makes n such calls. This upper bound, though correct, is not asymptotically tight. In reality, building a heap takes O(n) time depending on the implementation.

There may be two different ways to implement BUILD-HEAP

Start at the top of the heap (the beginning of the array) and call shiftUp on each item. At each step, the previously sifted items (the items before the current item in the array) form a valid heap and sifting the next item up places it into a valid position in the heap. After sifting up each node, all items satisfy the heap property.
Or, go in the opposite direction: start at the end of the array and move back towards the front. At each iteration, you shift an item down until it is in the correct location.

Where shiftDown and shiftUp is:

shiftDown swaps a node that is too small with its largest child (thereby moving it down) until it is at least as large as both nodes below it.
shiftUp swaps a node that is too large with its parent (thereby moving it up) until it is no larger than the node above it.

The logic does not produce a tight bound — it overestimates the complexity of each heapify. If built from the bottom up, insertion (heapify) can be much less than O(log(n)) .

The process is as follows:

( Step 1 ) The first n/2 elements go on the bottom row of the heap. h=0 , so heapify is not needed.

( Step 2 ) The next n/2² elements go on row 1 up from the bottom. h=1 , heapify filters 1 level down.

( Step i ) The next n/(2^i) elements go in row i up from the bottom. h=i , heapify filters i levels down.

( Step log(n) ) The last n/(2^log2(n)) = 1 element goes in row log(n) up from the bottom. h=log(n) , heapify filters log(n) levels down.

Note: After step one, 1/2 of the elements (n/2) are already in the heap, and we didn't even need to call heapify once. Also, notice that only a single element, the root, actually incurs the full log(n) complexity.

Theoretically

The Total steps N to build a heap of size n can be written out mathematically.

At height i , we've shown (above) that there will be n/(2^i+1) elements that need to call heapify, and we know heapify at height i is O(i) . This gives:

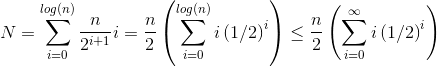
The solution to the last summation can be found by taking the derivative of both sides of the well known geometric series equation:

Finally, plugging in x = 1/2 into the above equation yields 2 . Plugging this into the first equation gives:

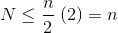
Thus, the total number of steps is of size O(n)

Solution steps

Convert the given array of elements into an almost complete binary tree.
Ensure that the tree is a max heap.

Check that every non-leaf node contains a greater or equal value element than its child nodes.
If there exists any node that does not satisfy the ordering property of max heap, swap the elements.
Start checking from a non-leaf node with the highest index (bottom to top and right to left).

Pseudo Code

void MaxHeapify(int arr[], int i, int n) 
{ 
    left = 2*i + 1
    right = 2*i + 2
    largest = i
    if (left < n and arr[left] > arr[i]) 
        largest = left
    if (right < n and arr[right] > arr[largest]) 
        largest = right
    if (largest != i) 
    { 
        swap(arr[i], arr[largest])
        MaxHeapify(arr, largest, n)
    } 
}

void convertMaxHeap(int arr[], int n) 
{ 
    // Start from bottommost and rightmost 
    // internal mode and heapify all internal 
    // modes in bottom up way 
    for (int i = (n-2)/2 to i >= 0) 
        MaxHeapify(arr, i, n)
}

Complexity Analysis

Time Complexity: O(n) (How?)

Space Complexity: O(log n), because of the stack space required for recursion.

Critical Ideas to Think

How building max heap uses O(n) time complexity instead of O(n log n)? Can you prove it mathematically?
Does the input array being a min-heap instead of randomly filled values affect the time complexity in the above approach?
If the input array is a max heap and the required output is a Min heap, Will the above approach will work? If yes, Why?