Binary Tree Zig Zag Level Order Traversal

Binary Tree Zigzag Level Order Traversal

Difficulty: Medium

Asked in: Amazon, Microsoft

Understanding the Problem

Given a binary tree, return the zigzag level order traversal of its nodes’ values. (i.e, from left to right, then right to left for the next level and alternate between).

Example

Input: Given binary tree [5,8,2,null,null,6,4]
    3
   / \
  9   20
     / \
    15  7
Output: Return its zigzag level order traversal as:
[
  [3],
  [20,9],
  [15,7]
]

The node structure passed to your function will be

class TreeNode
{
    int val
    TreeNode left
    TreeNode right
}

Solutions

Recursive Depth-first search approach: Make a DFS search from the root and for even levels reverse the list values at that level.
Iterative Level Order Traversal approach: Follow an iterative Level order traversal and for each level, poll the visited element from the Queue maintaining a boolean flag to toggle traversals.

You may try to solve this problem here.

1. Recursive Depth-First Search(DFS) Approach

If you will think about the problem, you will realize that this problem is basically a preorder or postorder traversal with the only difference that for each level, the traversal toggles between left to right and right to left.

However, the problems require to return a two-dimensional array that will contain the zig-zag traversal of the tree in a level order fashion.

So, We could create a res array and make a DFS or preorder tree traversal, while passing another argument called level . If the level is even, then we will add the root value in the res array in the end of the res[level] otherwise, at the beginning of res[level] . To reduce the time complexity of shifting, we can use an array of a doubly linked list and before returning, convert all the doubly linked lists into an array.

Example:

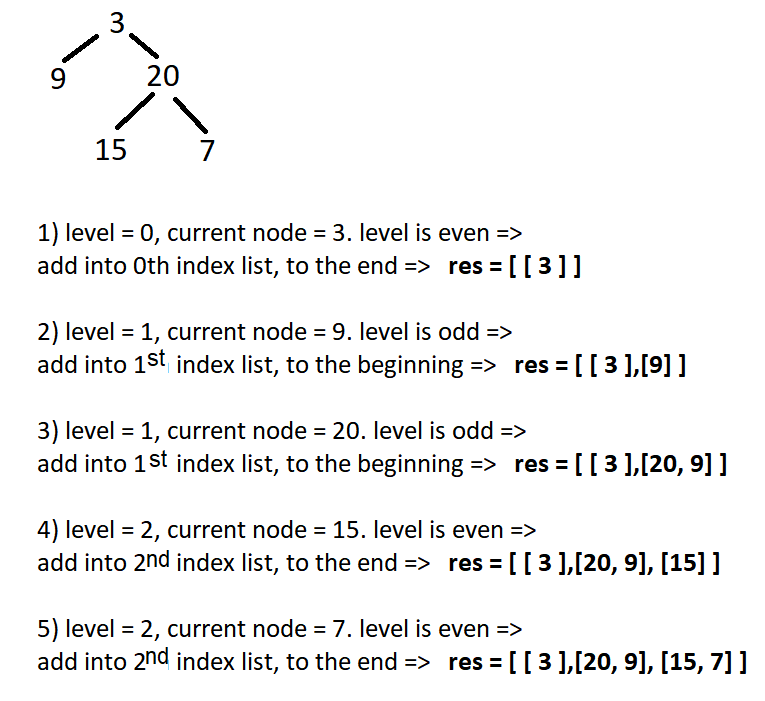
Solution step

Create an array of lists (this will be our output)
Call recursively DFS function that adds current node value to the output by level.
In your recursive call, use the level of this node in the tree as an argument.

If it’s even → Insert into the end of the list with index = level
if it’s odd → Insert into the beginning of list with index = level

int[][] zigzagLevelOrder(TreeNode root) {
    int[][] res
    zigzagLevelOrder(root, res, 0)
    return res
}
    
void zigzagLevelOrder(TreeNode root, int[][] res, int level) {
    if (root is not null){
        if (res.size() <= level)
            res.append([])
        if (level%2==0)
            res[level].append(root.val)  // Inserts at the end of the list
        else 
            res[level].insert(0, root.val) // Inserts at the beginning of the list
        zigzagLevelOrder(root.left, res, level+1)
        zigzagLevelOrder(root.right, res, level+1)
    }
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(n), the space complexity is the height of the tree , which in worst-case is n.

Critical Ideas to Think

How did we toggle from left to right and right to left traversal on each level?
Do you think that this algorithm could also be implemented by using postorder or inorder traversal? How?
How does the algorithm work if at any level there is only one node available? Check using a sample test case.

2. Iterative Level Order Traversal Approach

Solution steps

A better idea for ZigZag Level Order Traversal is the Breadth-First Approach that we use in a Level Order Traversal. Add a root node to Queue.
Iterate until the contents of the queue become empty.
Reset the level list on each level to a new array. On each level, pop the last visited element from the Queue.
A boolean flag could be useful that will help in toggle between the left to right and right to left traversal in the tree. A generalization could be for left to right traversal, flag is false, in which case simply add the polled node’s value to the level list, used for tracking the list of values on each particular level and vice versa.
Once a visited node’s value has been added to level list, explore it’s children if they exist.
If the entire level of nodes has been visited, add the level list to the final result list. Toggle flag to achieve zig zag level order traversing. Continue to iterate the aforementioned steps until the queue is completely empty.

Pseudo Code

int[][] zigzagLevelOrder(TreeNode root) {
    int[][] res
    if(root is null)
        return res
    //declare queue
    Queue(TreeNode) queue
    queue.add(root)
    boolean zigzag  = false
    while( queue is not Empty) {
        //declare level list and size from q 
        int[] level
        int size = queue.size()
        for (int i = 0 to i < size) {
            //poll from q
            TreeNode node = queue.pop()
            if (zigzag) {
                level.add(0, node.val)
            } else {
                level.add(node.val)
            }
            if (node.left is not null) {
                queue.add(node.left)
            }
            if (node.right is not null) {
                queue.add(node.right)
            }
        }
        res.add(level)
        zigzag = !zigzag
    }
    return res
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(n)

Critical Ideas to Think