Binary Search Tree: Introduction, Operations and Applications

Binary Search Tree is a special type of binary tree that has a specific order of elements in it. It follows three basic properties:-

  1. All elements in the left subtree of a node should have a value lesser than the node’s value.
  2. All elements in the right subtree of a node should have a value greater than the node’s value
  3. Both the left and right subtrees should be binary search trees too.

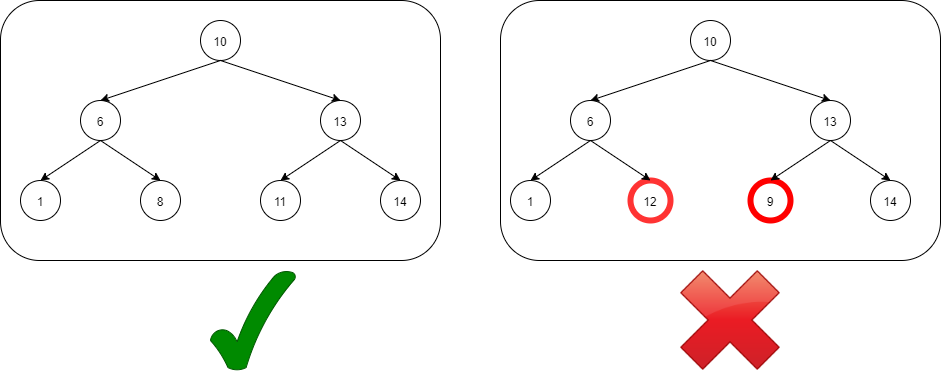
This is the simple structure followed by Binary Search Tree(BST). It is named so because it increases the efficiency of the search operation in a tree(logarithmic) just like in Binary Search.

Important Property: Inorder Traversal of BST returns a sorted arrangement of its values

Operations in BST

Since BST is a type of Binary Tree, the same operations are performed in BST too. Although, insertion and deletion in BST are much stricter with predetermined conventions so that even after performing an operation, the properties of BST are not violated.

1. Searching

Let us first see the main operation in BST → Searching.

In a normal binary tree, if we need to search for an element, we need to traverse the entire tree(in the worst case). But in BST, we can optimize this by using its properties to our advantage. Any guesses to how we can achieve that?

The basic idea is quite simple really. Let’s assume we need to search for value item in a BST. When we compare it with the root of the tree, we are left with three cases →

  • item == root.val: We terminate the search as the item is found
  • item > root.val: We just check the right subtree because all the values in the left subtree are lesser than root.val
  • item < root.val: Now we just check the left subtree as all values in the right subtree are greater than root.val

We keep on recursing in this manner and this decreases our search time complexity up to a great extent as we just need to look at one subtree and reject the other subtree saving us the trouble of comparing a batch of values.

Let’s implement this now.

Solution Steps

Our objective is to return True if a node exists with the value equal to the item, else return False .

  1. Check if the root is NULL, return False if it is NULL.
  2. Else, Compare root.val with item
  • item == root.val: return True
  • item > root.val: recurse for right subtree
  • item < root.val: recurse for left subtree
Pseudo-Code 
bool search(TreeNode root, int item)
{
    if ( root == NULL )
        return False
    
    if ( item == root.val )
        return True
    
    else if ( item > root.val )
        return search(root.right, item)
    
    else if ( item < root.val )
        return search(root.left, item)
}
Complexity Analysis

Upon Analyzing the execution of the above code, we can draw up the conclusion that we scan one level at a time. It works like a binary search in an array with the root acting like the middle element of the tree. We just look at left or right subtree saving us a lot of time. Once we compare the node we select, we move on to either the left or right subtree, hence, moving one level up.

→ Now, we can easily conclude that the worst-case time complexity is the highest level number possible which is equal to the total height of the tree(H).

★ Now, what is the height of BST in terms of N, the total number of nodes? Well, a height-balanced BST has a maximum height of logN .

But in a normal binary search tree, the worst-case time complexity of the searching operation is still O(N) , same as the binary tree.

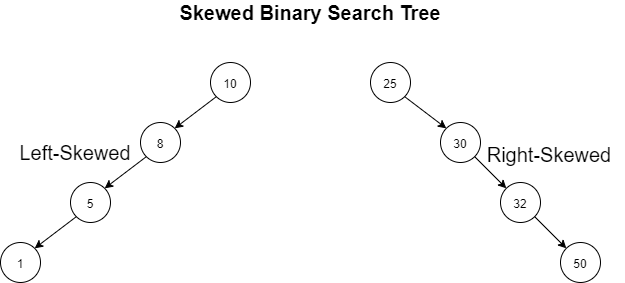
Can you guess the tree structure in the worst-case?

→ It's a left-skewed or right-skewed tree.

2. Insertion

Insertion in Binary Search Tree, just like Binary Tree is done at the leaf. But since it needs to maintain the properties of BST, the convention is decided in this case.

Solution Steps

We need to insert a node in BST with value item and return the root of the new modified tree.

  1. If the root is NULL, create a new node with value item and return it.
  2. Else, Compare item with root.val
  • If root.val < item , recurse for right subtree
  • If root.val > item , recurse for left subtree
Pseudo-Code 
TreeNode insert_element(TreeNode root, item)
{
    if ( root == NULL )
    {
        root = TreeNode(item)
        return root
    }
    if ( root.val < item )
        root.right = insert_element(root.right, item)
    else if ( root.val > item )
        root.left = insert_element(root.left, item)
    return root
}
Complexity Analysis

Since the new node is inserted at the leaf, the highest value possible for this is the height of the tree. And therefore, just like above the worst-case complexity for this is O(N) .

3. Deletion

When we delete a node in BST, we may encounter three cases →

  1. The node to be deleted is a leaf node : Easiest case, simply remove the node from the tree
  2. The node to be deleted has only one child : Replace the node by its child
  3. The node to be deleted has both children : The node still needs to be replaced to maintain BST properties, but which node should replace this deleted node?

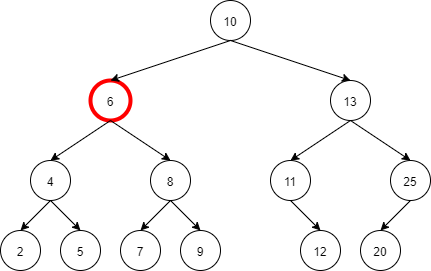
Suppose we have to delete the node with value 6, which node should be selected ideally to replace this node?

→ The inorder successor of this node would be the aptest choice to replace this node as its inorder successor is the smallest element that is greater than this node.

Note: The inorder predecessor can be used to replace this node too. But conventionally, we use the inorder successor to replace the node.

Solution Steps

You need to delete the node with value item and then return the root of the modified tree. First, we need to find the node to be deleted and then replace it by the appropriate node if needed.

  1. Check if the root is NULL, if it is, just return the root itself. It's an empty tree!
  2. If root.val < item , recurse the right subtree.
  3. If root.val > item , recurse the left subtree.
  4. If both above conditions above false, this means root.val == item .
  5. Now we first need to check how many child did root have.
  6. CASE 1: No Child → Just delete root or deallocate space occupied by it
  7. CASE 2: One Child →Replace root by its child
  8. CASE 3: Two Children
  • Find the inorder successor of the root (Its the smallest element of its right subtree). Let's call it new_root.
  • Replace root by its inorder successor
  • Now recurse to the right subtree and delete new_root.

9. Return the root .

Pseudo-Code 
TreeNode delete_element(TreeNode root, int item)
{
    if ( root == NULL )
        return root
    
    if ( root.val < item)
        root.right = delete_element(root.right, item)
    else if ( root.val > item )
        root.left = delete_element(root.left, item)
    else if ( root.val == item )
    {
        // No child
        if ( root.left == NULL and root.right == NULL )
            delete root
        // Only one child
        else if ( root.left == NULL or root.right == NULL )
        {
            if(root.left != NULL)
            {
                TreeNode new_root = root.left
                delete root
                return new_root
            }
            else
            {
                TreeNode new_root = root.right
                delete root
                return new_root
            }
        }
        // Both left and right child exist
        else
        {
            TreeNode new_root = find_inorder_successor(root.right)
            root.val = new_root.val
            root.right = delete_element(root.right, new_rot.val)
        }
    }
    return root
}
TreeNode find_inorder_successor(TreeNode root)
{
    TreeNode curr = root
    while ( curr.left != NULL )
        curr = curr.left
    
    return curr
}

★ Don’t forget to deallocate memory according to the requirements of the programming language of your choice.

Complexity Analysis

Deletion has similar complexity as insertion because, in this, the worst case is that the node to be deleted is a leaf node or else it has two children and the inorder successor will be at the highest level. Therefore, for deletion too, the worst-case time complexity is O(N) .

Variations

There are certain variations applied to Binary Search Trees to improve efficiency for certain common operations such as insertion, deletion, etc.

  • AVL Trees
  • Red-Black Trees

These two are the two most common self-balancing BSTs which allow us to optimize the height of BSTs by changing the structure of BST such that it accommodates all the nodes in a BST tree with minimum height possible.

Applications of BST

BSTs are used for a lot of applications due to its ordered structure.

  • BSTs are used for indexing and multi-level indexing.
  • They are also helpful to implement various searching algorithms.
  • It is helpful in maintaining a sorted stream of data.
  • TreeMap and TreeSet data structures are internally implemented using self-balancing BSTs

Happy Coding!