All Nodes Distance K in Binary Tree

Difficulty: Medium

Companies: Microsoft

Understanding The Problem

Problem Description

We are given a binary tree with root node root, a target node target , and an integer value k . Write a program to return a list of the values of all nodes that have a distance k from the target.

Problem Note →

The answer can be returned in any order.
The given tree is non-empty.
Each node in the tree has unique values.
The target node is a node in the tree.

Given the following binary tree: root = [5, 6, 3, 1, 7, 9, 4, null, null, 2, 0]

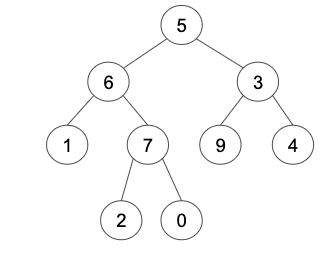
Example 1

Input: root = [5, 6, 3, 1, 7, 9, 4, null, null, 2, 0], target = 6, K = 2
Output: [2,0,3]
Explanation: The nodes that are a distance 2 from the target node with value 6 have values 2, 0, and 3.

The node structure passed to your function will be

class TreeNode
{
    int val
    TreeNode left
    TreeNode right
}

Solutions

Convert Tree into Graph: Create a hashmap of nodes and their parents. Perform BFS from the target node and add all nodes at distance K to result.
Percolate Distance: Perform DFS from the root and check for the distance of target node distance from each node.

You may try this problem here.

1. Convert Tree into Graph

The question says, that we have to find out all the nodes that are at a distance of K from the target node. If you are able to imagine that the given directed binary tree to be an undirected graph, then we could perform a BFS search from the target nodes up to the distance K, then it would be our answer.

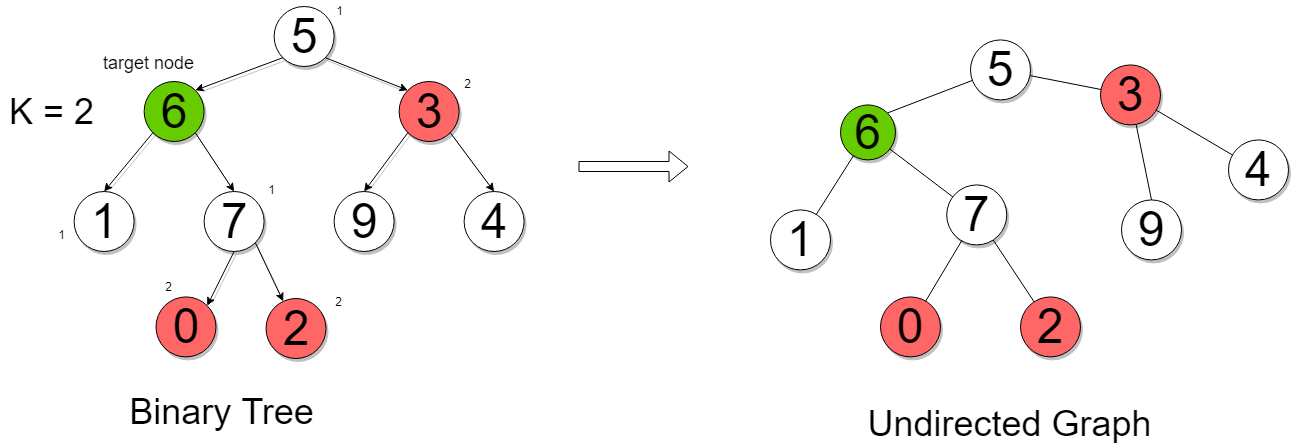
Solution steps

Create a graph from the given tree.

The graph can be adjacency list or adjacency matrix
You can build the graph by making a postorder traversal of the tree.

2. Then from the target node, make a BFS search up to a distance k from the target node and store the kth nodes in the result array.

3. Now simply return the result array.

Pseudo Code

class Solution {
public:
    // Graph is an adjacency list
    map(int, []) Graph
    int[] ans
    
    void buildGraph(TreeNode node, TreeNode parent) {
        if (not node) 
            return
        if (not Graph.count(node.val)) {
            if (parent) {
                Graph[node.val].add(parent.val)
                Graph[parent.val].add(node.val)
            }
            buildGraph(node.left, node)
            buildGraph(node.right, node)
        }
    }
    
    void bfs(TreeNode target, int k) {
        queue q
        // visited map of int : bool
        map <int, bool> visited
        int depth = 0
        if (k == 0) {
            ans.add(target.val)
            return
        }
        q.push(target.val)
        while (not q.empty()) {
            depth = depth + 1
            int q_size = q.size()
            for (int i=0 to i<q_size) {
                int curr_node = q.front()
                visited[curr_node] = true
                q.pop()
                for (int neighbour in Graph[curr_node]) {
                    if (not visited.count(neighbour)) {
                        if (depth == k) 
                            ans.add(neighbour)
                        else 
                            q.push(neighbour)
                    }
                }
            }
            if (depth == k) 
                return
        }
    }
    
    int[] distanceK(TreeNode root, TreeNode target, int K) {
        buildGraph(root, nullptr)
        bfs(target, K)
        return ans
    }
}

Complexity Analysis

Time Complexity: O(n)

Space Complexity: O(n)

Critical Ideas to Think

How did we convert the binary tree into an undirected graph?
Did we use the adjacency list to create the graph?
Why did we perform the BFS up to the distance k from the target node?
Can we solve this problem using the adjacency matrix?

2. Percolate Distance

The problem can also be solved with the help of recursion. If we will just try to traverse the tree and check if the current node during traversal is the target node. If its a target node, then simply get the nodes by performing a preorder traversal like subtree_add function in pseudo-code up to a distance k while considering the target node as the root. If the node is not the target node, then we could check if the target node is in the left subtree or in the right subtree.

As soon as we determine that the target node is in the left subtree, then we will go to the right subtree and add the nodes at a distance K from the target node and if the target node is in the right, then we will traverse to the left. Consider the following example →

From root , say the target node is at depth 3 in the left branch. It means that any nodes that are distance K - 3 in the right branch should be added to the answer.

Solution Steps

Traverse every node with a depth-first search. We'll add all nodes x to the answer such that node is the node on the path from x to target that is closest to the root .
dfs(node) will return the distance from node to the target . Then, there are 4 cases:

If node == target , then we should add nodes that are distance K in the subtree rooted at target .
If target is in the left branch of node , say at a distance L+1 , then we should look for nodes that are distance K - L - 1 in the right branch.
If target is in the right branch of node , the algorithm proceeds similarly.
If target isn't in either branch of node , then we stop.

Pseudo Code

class Solution {
    int[] ans
    TreeNode target
    int k
    int[] distanceK(TreeNode root, TreeNode Target, int K) {
        target = Target
        k = K
        dfs(root)
        return ans
    }

   // Return vertex distance from node to target if exists, else -1
    int dfs(TreeNode node) {
        if (node is null)
            return -1
        else if (node is target) {
            subtree_add(node, 0)
            return 1
        } else {
            int L = dfs(node.left)
            R = dfs(node.right)
            if (L != -1) {
                if (L == K)
                   ans.add(node.val);
                subtree_add(node.right, L + 1)
                return L + 1
            } else {
                if (R != -1) {
                    if (R == K) ans.add(node.val)
                    subtree_add(node.left, R + 1)
                    return R + 1
                } else {
                    return -1
                }
            }
        }
    }

   // Add all nodes 'K - dist' from the node to answer.
    void subtree_add(TreeNode node, int dist) {
        if (node is null) 
            return
        if (dist is K)
            ans.add(node.val)
        else {
            subtree_add(node.left, dist + 1)
            subtree_add(node.right, dist + 1)
        }
    }
}

Complexity Analysis

Time Complexity: O(n) (How?)

Space Complexity: O(n), due to recursive stack space

Critical Ideas to Think

How did we check if the target node is in the left or the right subtree from the current node during DFS traversal?
How did we able to find out, what distance is the target node from the current node in constant time during the DFS traversal?
What does subtree_add function represent here?